EMTEST 25 listopada 2021 r.

Matematyka dla Stowarzyszenia Elektrotechników Polskich w RC

Temat prelekcji:

„Matematyka – niezbędne narzędzie elektrotechniki”

(Krótka rozrywka językowa)

Przy otwieraniu tego pliku wyskoczy u góry zapytanie czy tak lub nie, proszę wybrać nie!

Odmiana przez przypadki rzeczownika pan; rzeczownik; forma grzecznościowa stosowana przy zwracaniu się do mężczyzn.

Przypadek	Liczba pojedyncza	Liczba mnoga
Mianownik (kto? co?):	pan	panowie pany
Dopełniacz (kogo? czego?):	pana	panów
Celownik (komu? czemu?):	panu (nie panowi!)	panom
Biernik (kogo? co?):	pana	panów
Narzędnik (z kim? z czym?):	panem	panami
Miejscownik (o kim? o czym?):	panu (nie panowi!)	panach
Wołacz (hej!):	panie!	panowie pany

Zwracamy się: proszę pana! Nie mówimy i nie piszemy: to pański pies? Ale to pana pies?

Odmiana przez przypadki rzeczownika pani

pani; rzeczownik; forma grzecznościowa stosowana przy zwracaniu się do kobiet.

Przypadek	Liczba pojedyncza	Liczba mnoga
Mianownik (kto? co?):	ta pani	panie
Dopełniacz (kogo? czego?):	tej pani	pań
Celownik (komu? czemu?):	tej pani	paniom
Biernik (kogo? co?):	tę panią	panie
Narzędnik (z kim? z czym?):	z tą panią	paniami
Miejscownik (o kim? o czym?):	tej pani	paniach
Wołacz (hej!):	(O!) pani	panie

Proszę pani (grzecznościowe zwracanie się do kobiety),

ale proszę panią o pomoc, o napisanie listu.

Jak odmieniać wyraz dwuznaczny państwo?

Już sam przypadek ma dwie formy w dopełniaczu liczby pojedynczej: przypadku i przypadka (przy używaniu go przy odmianie przez przypadki)

Tutaj chodzi o odmianę wyrazu państwo (kraj), państwo polskie, czeskie itp.

przypadek	liczba pojedyncza
mianownik	państwo
dopełniacz	państwa
celownik	państwu
biernik	państwo
narzędnik	państwem
miejscownik	o państwie
wołacz	państwo

A tutaj chodzi o najwyższą formę grzecznościową z użyciem wyrazu państwo

przypadek	liczba mnoga
mianownik	państwo
dopełniacz	państwa
celownik	państwu
biernik	państwa
narzędnik	państwem
miejscownik	o państwu
wołacz	państwo

Między przymiotnikiem „szanowni” i rzeczownikiem „państwo” zachodzi związek rządu, tzn. pierwszy przyjmuje formę pluralną (mnogą), mimo że łączy się z rzeczownikiem liczby pojedynczej rodzaju nijakiego.

M. (kto? co?) szanowni państwo,

D. (kogo? czego?) szanownych państwa
C. (komu? czemu?) szanownym państwu
B. (kogo? co?) szanownych państwa
N. (z kim? czym?) z szanownymi państwem
Ms. (o kim? o czym?) o szanownych państwu.

W. (O!) szanowni państwo!

(kto? co?) ci Szanowni Państwo Młodzi

(kogo? czego?) tych Szanownych Państwa Młodych

(komu? czemu?) tym Szanownym Państwu Młodym

(kogo? co?) tych Szanownych Państwa Młodych

(z kim? czym?) z tymi Szanownymi Państwem Młodymi

6. Msc. (o kim? o czym?) o tych Szanownych Państwu Młodych

7. Wołacz (O!) Szanowni Państwo Młodzi!

Na koniec zapamiętajmy poprawne formy wyrażenia państwo młodzi (nowożeńcy’), gdyż często nie umieją sobie z nimi poradzić w odmianie różni wodzireje i muzykanci podczas przyjęć weselnych.

Mówi się i pisze najpoprawniej: widzą państwo, pamiętają państwo, pozwol

ą państwo itp., czyli orzeczenie przyjmuje postać 3. osoby liczby mnogiej.

Pięknie wyglądają państwo młodzi;

Nie ma jeszcze państwa młodych;

Państwu młodym się nie odmawia;

Należy przywitać państwa młodych;

Zrobić sobie zdjęcie z państwem młodymi (a nie: z państwem młodym ani państwem młodych);

Opowiadano z zachwytem o państwu młodych (nie: o państwie młodym ani o państwie młodych).

W formie grzecznościowej Szanowni Państwo, jak również i do znaczących osobistości, np. Szanowny Panie Profesorze, należy zwracać się w listach, nie zapominając, iż wszystkie litery początkowe tych zwrotów powinny być napisane literą wielką!

Sformułowania: widzicie państwo, pamiętacie państwo, pozwolicie państwo itp. długo były traktowane przez językoznawców jako niepoprawne – dzisiaj dopuszczane są jako mniej poprawne, praktyczniejsze

https://obcyjezykpolski.pl/witamy-szanownych-panstwa/

Proszę pamiętać o użyciu drugiego przypadka w przeczeniach!

Mam książkę. Nie mam książki! Nie mam czasu! Mnie tam nie było!

Niech zauważą Szanowni Państwo (dalej już tutaj koledzy), gdzie jest

w języku polskim akcent w wyrazach:

ogólnie twierdzi się, iż jest na przedostatniej sylabie, a jednak nie zawsze!

myliśmy, pracowaliśmy, mówiliśmy, a nie płakaliśmy, liczyliśmy wędziliśmy,

ale robiłbym, robiliby, robilibyśmy,

napisalibyśmy, zjedlibyście,

gdzie pada akcent w wyrazie nauka? Prezydent,

matematyka, fizyka, polityka, logika pedagogika, muzyka, elektrotechnika,

Proszę uważać też na koniugację czasowników niektórych czasowników w piewszej osobie liczby pojedynczej!

ja jem, umiem, rozumiem (a nie: ję, umię, rozumię)!

--------------------

Systemy liczbowe (Číselné systémy)

System liczbowy – zbiór (množina) reguł jednolitego zapisu i nazewnictwa liczb. Do zapisywania liczb używa się skończonego zbioru znaków, zwanych cyframi, które można łączyć w dowolnie długie ciągi, otrzymując nieskończoną liczbę kombinacji.

CYFRA, LICZBA, ILOŚĆ (ČÍSLICE, ČÍSLO, MNOŽSTVÍ)

Cyfra jest znakiem graficznym. Cyfr arabskich jest dziesięć:

0, 1, 2, 3, 4, 5, 6, 7, 8 i 9, a dziś używanych rzymskich siedem:

I, V, X, L, C, D, M.*

Liczba oznacza "stan liczebny" albo pojęcie, którego treścią jest wynik liczenia wyrażony zwykle cyframi. Liczba odnosi się więc do rzeczy "policzalnych", przedmiotów (żywych i martwych), które można kolejno policzyć. Ilość jest miarą tego, co może być mierzone lub ważone, to jest odnosi się do rzeczy "niepoliczalnych", np. gazów, cieczy, ciał sypkich, pojęć abstrakcyjnych itp.

Należy pisać: liczba ludzi, liczba pomysłów, liczba krwinek płytkowych, liczba książek. Ilość mąki, ilość powietrza, ilość białka, ilość rozumu.

Nie należy używać: ilość ludzi, cyfra dwadzieścia trzy (to dwie cyfry!)

Rodzaje liczb (Druhy čísel)

Liczby naturalne (Přírozená čísla)

Liczby naturalne – to liczby całkowite, dodatnie:

1,2,3,4,5,6,...

Czasami do liczb naturalnych zaliczamy również liczbę zero (autor książki matematycznej powinien zawsze jasno określić, czy uznaje liczbę zero za naturalną, czy też nie!).

Zbiór (mnogość elementów, pojęcie pierwotne, aksjomat) liczb naturalnych oznaczamy literą N.
Możemy zapisać, że:

N={1,2,3,4,5,6,...}

Jeżeli zakładamy, że zero również jest liczbą naturalną, to zapiszemy:

N={0,1,2,3,4,5,...}

Czasami dla zbioru liczb naturalnych dodatnich stosujemy oznaczenie N+.

N+={1,2,3,4,5,6,...}

Ten sam zbiór możemy również zapisać wykorzystując symbol liczb całkowitych:

Z+={1,2,3,4,5,6,...}

(nawiasy okrągłe, kwadratowe, klamrowe, ostrokątne)

Liczby całkowite (Celá čísla)

Liczby całkowite ─ to liczby naturalne oraz ich ujemne odpowiedniki, a także liczba zero:

...−6,−5,−4,−3,−2,−1, 0, 1, 2, 3, 4, 5, 6, ...

Zbiór liczb całkowitych oznaczamy symbolem Z.

Z={...−6,−5,−4,−3,−2,−1, 0, 1, 2, 3, 4, 5, 6, ...}

Zbiór liczb całkowitych dodatnich to:

Z+ = {1, 2, 3, 4, 5, 6, ...}

Możemy także zapisać zbiór liczb całkowitych ujemnych:

Z− = {...−6,−5,−4,−3,−2,−1} (z niemieckiego ganze Zahlen)

Zbiór liczb całkowitych dodatnich, to zbiór liczb naturalnych.

Liczby wymierne (Racionální čísla)

Liczba wymierna – to taka liczba, którą można zapisać w postaci ułamka zwykłego, czyli w postaci:

p/q

gdzie: p - to dowolna liczba całkowita
q - to liczba całkowita różna od 0 (ponieważ nie wolno dzielić przez zero!).

Zbiór liczb wymiernych oznaczamy symbolem Q.

Formalnie zbiór liczb wymiernych można zapisać w taki sposób:

Q = {p/q:p,q∈Z∧q≠0}

Przykład 1.

Liczba 3/4 jest wymierna, ponieważ jest zapisana w postaci ułamka zwykłego.

Twierdzenie 1. Każda liczba całkowita jest wymierna.

Każdą liczbę wymierną można zapisać za pomocą ułamka na dowolnie wiele sposobów.

Przykład 2.

Liczba 1 jest wymierna, ponieważ można ją zapisać w postaci ułamka zwykłego:

1/1 = 4/4 = 11/11 = 4/4 = 17/17 = 1

Przykład 3.

Liczba 5 jest wymierna, ponieważ można ją zapisać w postaci ułamka zwykłego:

5/1 = 10/2 = 60/12 = 5:1 = 5

Przykład 4.

Liczba −3 jest wymierna, ponieważ można ją zapisać w postaci ułamka zwykłego:

−3/1 =−6/2 = 900/300 = 3

Przykład 5.

Liczba 0 jest wymierna, ponieważ można ją zapisać w postaci ułamka zwykłego:

0/1 = 0/2 = 0/3 = 0

Przykład 6.

Liczba 17/8 jest wymierna, ponieważ można ją zapisać w postaci ułamka zwykłego:

17/8 = 15:8

Przykład 7.

Liczba 0,(3) jest wymierna, ponieważ można ją zapisać w postaci ułamka zwykłego:

0,(3) = 1/3 = 0,33333 (okres 3)

Przykład 8.

Liczba 4^1/2jest wymierna, ponieważ można ją zapisać w postaci ułamka zwykłego:

4^1/2 = 2 = 2/1

Przykład 9.

Liczba 125^1/3 jest wymierna, ponieważ można ją zapisać w postaci ułamka zwykłego:

125^1/3 = 5 = 5:1

Liczba w liczniku ułamka wykładnika oznacza stopień potęgi,

w mianowniku oznacza stopień pierwiastka!

Liczby niewymierne (Iracionální čísla)

Liczba niewymierna to taka liczba, której nie można zapisać za pomocą ułamka zwykłego.

Przykład 1.

(x^5/3) = to są dwa sposoby zapisów identycznych

Liczbami niewymiernymi są np.:

2^1/2, 3^1/2, 5^1/2, 17^1/2, 2^1/3, π, e...

Żadnej z tych liczb nie da się zapisać w postaci ułamka zwykłego!

Liczba Ludolfa π = 3,14159265359 ;

Liczba Eulera e = 2,71828182845904523536028747135266249775724709.

Uwaga! Nie każdy pierwiastek jest liczbą niewymierną, np.:

9^1/2 = 3 = 3/1

Suma liczby wymiernej i niewymiernej jest zawsze liczbą niewymierną!

Iloczyn (mnożenie) dwóch liczb niewymiernych może być liczbą wymierną albo niewymierną!

liczba 2^1/2. 2^1/2 = 4^1/2=2 jest wymierna

2^1/2 .3^1/2= 6^1/2 niewymierna

Liczby rzeczywiste (Reálná čísla)

Liczby niewymierne wraz z liczbami wymiernymi tworzą zbiór liczb rzeczywistych

Zbiór liczb rzeczywistych oznaczamy symbolem R

Liczbami rzeczywistymi są, np.:

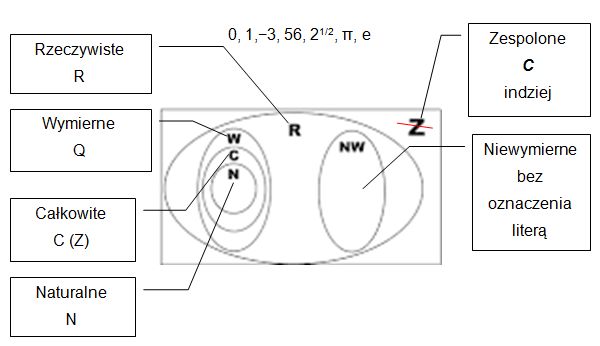Potęgi:

Przykłady:

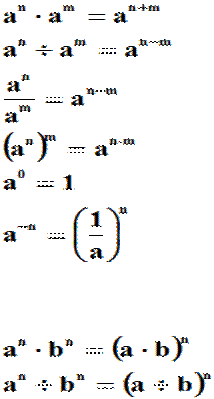
Pierwiastki

Przykłady:

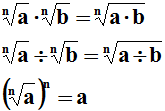
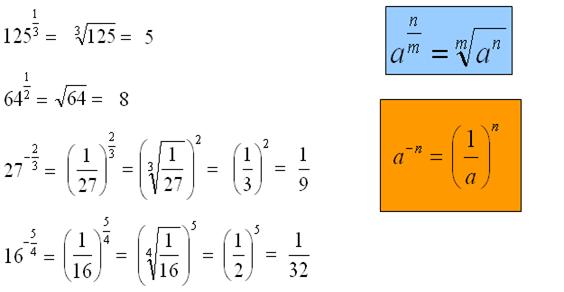
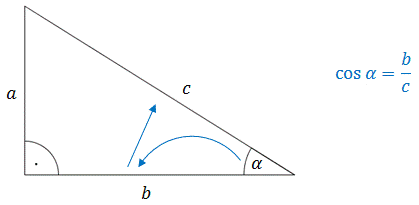
Definicje funkcji trygonometrycznych kąta ostrego - metoda graficzna do zapamiętania

Aby obliczyć sinus kąta ostrego w trójkącie prostokątnym

(v pravoúhlém trojúhelníku), to:

patrzymy najpierw na bok naprzeciwko kąta,

potem na przeciwprostokątną.

Aby obliczyć cosinus kąta ostrego w trójkącie prostokątnym, to:

patrzymy najpierw na przyprostokątną przy kącie,

Aby obliczyć tangens kąta ostrego w trójkącie prostokątnym, to:

patrzymy najpierw na bok naprzeciwko kąta,

potem na drugą przyprostokątną.

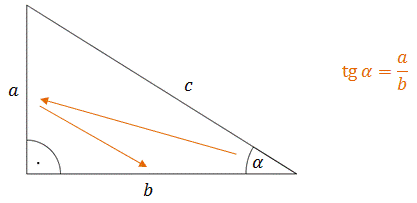
Aby obliczyć cotangens kąta ostrego w trójkącie prostokątnym, to:

patrzymy najpierw na przyprostokątną przy kącie,

potem na drugą przyprostokątną.

Zależności między funkcjami trygonometrycznymi kątów ostrych w trójkącie prostokątnym

Twierdzenie 1. Funkcje trygonometryczne kąta ostrego w trójkącie prostokątnym są dodatnie.
Uzasadnienie:

Funkcje trygonometryczne kątów ostrych w trójkącie prostokątnym obliczamy jako stosunki odpowiednich boków danego trójkąta. Boki trójkąta mają zawsze długość dodatnią, zatem ich stosunki również są dodatnie.

Twierdzenie 2. Tangens i cotangens są swoimi odwrotnościami, czyli:

ctgα = 1/tgα

albo inaczej:

tgα⋅ctgα = 1

Twierdzenie 3. Dla trójkąta prostokątnego:

[obrazek - fakt 3]

mamy:

sinα = cosβ

cosα = sinβ

tgα = ctgβ

ctgα = tgβ

Uzasadnienie:

Korzystając bezpośrednio z definicji funkcji trygonometrycznych otrzymujemy:

sinα = a/c cosα = b/c

tgα = a/b ctgα = b/a

oraz

sinβ = b/c cosβ = a/c

tgβ = b/a ctgβ = a/b

Zatem mamy:

sinα = a/c = cosβ

cosα = b/c = sinβ

tgα = a/b = ctgβ

ctgα = b/a = tgβ

Twierdzenie 4. W trójkącie prostokątnym:

[obrazek - fakt 4] mamy:

β = 90°−α

Zatem:

sinα = cos(90°–α)

cosα = sin(90°−α)

tgα = ctg(90°−α)

ctgα = tg(90°−α)

Powyższe wzory to są tzw. wzory redukcyjne dla kąta 90°–α. Otrzymaliśmy je bezpośrednio z równości podanych w Twierdzeniu 3.

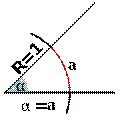
Okrąg jednostkowy (jednotková kružnice) (o promieniu r = 1)

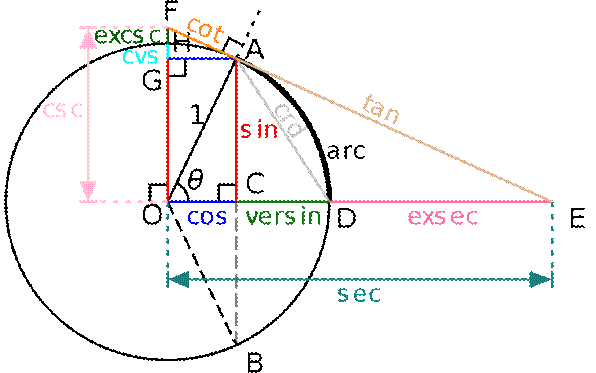
Na tym okręgu jednostkowym o promieniu 1 można zobaczyć dużą liczbę jego własności: funkcje sinus, cosinus, tangens, cotangens, arcsin, arccosinus, sekans, kosekans..., funkcje miar łukowych (arcus) oraz już bardzo mało używane funkcje, jak np. versinx = (1 – cosx). Miara łukowa kąta była wprowadzona w 1714 roku, o wiele później niż miara kątowa w stopniach (w starej Babilonii (1792–1750 p.n.e.), różnica 3 506 lat.

Równanie okręgu jednostkowego

x² + y² = 1

Miara kąta – wielkość kąta wyrażona w odpowiednich jednostkach. W matematyce i

jej zastosowaniach teoretycznych używa się miary łukowej.

Jest to długość łuku wyciętego przez kąt z okręgu o promieniu 1 i środku w wierzchołku kąta. Tak określona miara wyraża się liczbą niemianowaną (bezwymiarową) i może przyjmować wartości z zakresu 0 do 2π. Jednostkę miary łukowej nazywamy radianem.

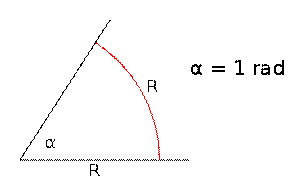
Kąt α ma miarę 1 radiana, jeśli długość łuku równa jest promieniowi R.

https://upload.wikimedia.org/wikipedia/commons/4/4e/Circle_radians.gif

W życiu codziennym używa się zwykle miary stopniowej. Kąt pełny dzieli się na 360 stopni kątowych (symbol: °), każdy z nich na 60 minut kątowych (symbol: ′), a każdą z nich na 60 sekund kątowych (symbol: ″). Ułamki sekund kątowych podawane są już dziesiętnie.

Tę właśnie miarę wykorzystuje się w popularnych kątomierzach.

W praktyce militarnej i geodezyjnej stosowany bywa podział kąta pełnego na 400 gradów (lub gradusów, symbol: ^g), z których każdy dzieli się na 100 centygradów (symbol: ^c), a każdy z nich na 100 myriogradów (symbol: ^cc). Podział taki ułatwia ręczne (pisemne) dodawanie i odejmowanie, ponieważ przeniesienia i pożyczki wykonuje się jak przy zwykłych liczbach dziesiętnych, bez konieczności przeliczania na 60 i 90 jednostek.

W pomiarach nachylenia nawierzchni

Kąt	Tangens	Sinus
0°	0 %	0 %
5°	9 %	9 %
10°	18 %	17 %
30°	58 %	50 %
45°	100 %	71 %
60°	173 %	87 %
90°	∞	100

używa się miary procentowej (np. przy określeniu nachylenia nawierzchni drogi). Przykładowo 1% (w języku polskim znak procentu % stawia się zaraz obok liczby!)

1 procent oznacza zmianę wysokości o 1 cm na 100 cm długości.

Miara kąta potocznie nazywana jest kątem.

Zamiana stopni na radiany i odwrotnie radiany na stopnie

Stopnie możemy bardzo łatwo zamieniać na radiany za pomocą proporcji. Wystarczy, że pamiętamy, np. zależność: 360° = 2π (rad).

Przykład 1.

Wyraź za pomocą radianów kąt o mierze 60°

Rozwiązanie:

Układamy proporcję:

360° = 2π (rad)

60° = x (rad)

x(rad)/2π = 60°/360°

x = 2π 60/360

x(rad) = 2 razy. 3,14 60/360 = 1,046666 rad

x(rad) = 1,046666 rad

1 radian =360°/2π ≈ 57°

Dokładnie 1 radian = 57·17′45′′

deg = rad⋅180/π.

rad = deg.π/180

Radiany możemy zamieniać na stopnie za pomocą proporcji.

Wystarczy, że pamiętamy np. zależność: 360° = 2π (rad)

Wyraź za pomocą stopni kąt o mierze łukowej (π/5).

x° = π/5x360/6,28 = 3,14/5x360/6,28 = 36°

x° = (rad) 360/2π

deg = rad⋅180/π

Wykresy funkcji trygonometrycznych oraz wzory trygonometryczne

Rozwiązania podstawowych równań trygonometrycznych, liczba (Z)

Funkcje trygonometryczne kąta ostrego

Funkcje trygonometryczne kąta ostrego

Wartości funkcji trygonometrycznych wybranych kątów ostrych

Funkcje trygonometryczne dowolnego kąta (skierowanego – orientovaného)

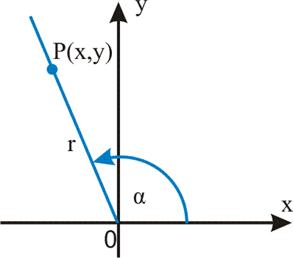
Funkcje trygonometryczne dowolnego kąta (skierowanego)

Własności funkcji trygonometrycznych miara główna

Funkcja	Własność	Warunek	Dziedzina
	nieparzysta
	parzysta
	nieparzysta
	nieparzysta

Okresowość funkcji trygonometrycznych, liczba (Z)


Funkcja	Okres podstawowy	Warunek

Jedynki trygonometryczne

Związki między funkcjami trygonometrycznymi

Wzory redukcyjne, Liczba

Funkcje trygonometryczne sumy i różnicy kątów

Funkcje trygonometryczne kąta podwojonego

Funkcje trygonometryczne kąta potrojonego

Suma i różnica takich samych funkcji trygonometrycznych

Funkcje trygonometryczne połowy kąta

Funkcje trygonometryczne wyrażone przez tangens połowy kąta

Związki między funkcjami cyklometrycznymi

Dla	Dla


Dla	Dla

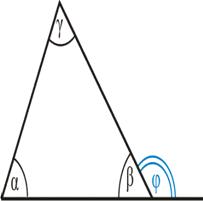
Trójkąt ogólny

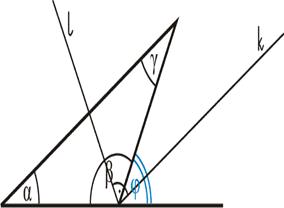
Kąt zewnętrzny trójkąta

Kąt zewnętrzny a kąt wewnętrzny

Kąt zewnętrzny jako suma kątów wewnętrznych

katy w trójkącie, kąt zewnętrzny i wewnętrzny

suma kątów wewnętrznych w trójkacie

dwusieczne

Obrazek ten jest wadliwy!

Związki miarowe w trójkącie

związki miarowe w trójkącie

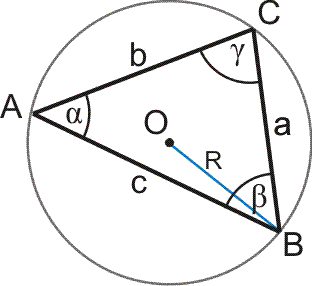
Twierdzenie sinusów (Snelliusa)	Twierdzenie kosinusów (Carnota)

Proszę o dokładne prześledzenie przebiegu funkcji trygonometrycznych

sinusa, cosinusa, tangensa i cotangensa

w zależności od miary kąta, na okręgu jednostkowym.

W edukatorze, proszę sobie wybrać sukcesywnie jedną

z czterech funkcji trygonometrycznych i uchwytem z kółkiem kręcić

i śledzić ich przebieg

https://www.edukator.pl/tik_edukator/Okrag_jednostkowy/index.html

Proszę zaznajomić się również z symbolami i znaczeniami matematycznymi w języku czeskim.

https://cs.wikipedia.org/wiki/Matematick%C3%A9_symboly_a_zna%C4%8Dky

i polskim oraz ubogacić swoją terminologię matematyczną w obu językach.

https://pl.wikipedia.org/wiki/Lista_symboli_matematycznych

Niektóre funkcje trygonometryczne wyrażone za pomocą szeregu Taylora

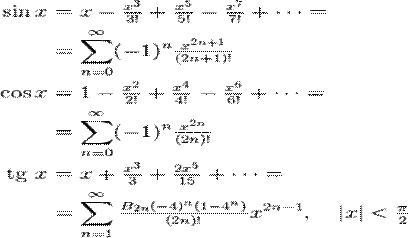
$\begin{align}\sin x &= x - \tfrac{x^3}{3!} + \tfrac{x^5}{5!} - \tfrac{x^7}{7!} + \cdots =\\&=\sum_{n=0}^\infty (-1)^n\tfrac{x^{2n+1}}{(2n+1)!}\\\cos x &= 1 - \tfrac{x^2}{2!} + \tfrac{x^4}{4!} - \tfrac{x^6}{6!} + \cdots =\\&=\sum_{n=0}^\infty(-1)^n\tfrac{x^{2n}}{(2n)!}\\\mbox{tg}\ x &= x + \tfrac{x^3}{3} + \tfrac{2 x^5}{15} + \cdots =\\&=\sum^{\infin}_{n=1} \tfrac{B_{2n} (-4)^n (1-4^n)}{(2n)!} x^{2n-1},\quad |x|<\tfrac{\pi}{2}\end{align}$

gdzie $B_n\;$ to liczby Bernoulliego

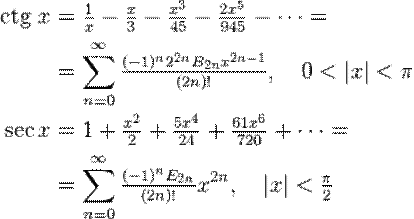
$\begin{align}\mbox{ctg}\ x&= \tfrac {1} {x} - \tfrac {x}{3} - \tfrac {x^3} {45} - \tfrac {2 x^5} {945} - \cdots =\\&=\sum_{n=0}^\infty \tfrac{(-1)^n 2^{2n} B_{2n} x^{2n-1}}{(2n)!},\quad 0 < |x| < \pi\\\sec x &= 1 + \tfrac {x^2} {2} + \tfrac {5 x^4} {24} + \tfrac {61 x^6} {720} + \cdots =\\&=\sum^{\infin}_{n=0} \tfrac{(-1)^n E_{2n}}{(2n)!} x^{2n},\quad |x|< \tfrac{\pi}{2}\end{align}$

gdzie $E_n\;$ to liczby Eulera

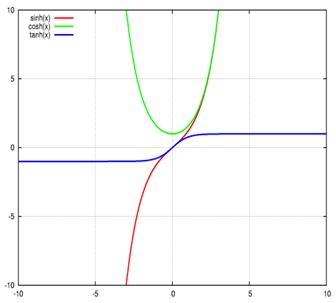
Funkcje hiperboliczne (Hyporbolické funkce)

Funkcje hiperboliczne to funkcje, których wartości powstają poprzez różne kombinowanie z wartościami funkcji , a konkretnie:

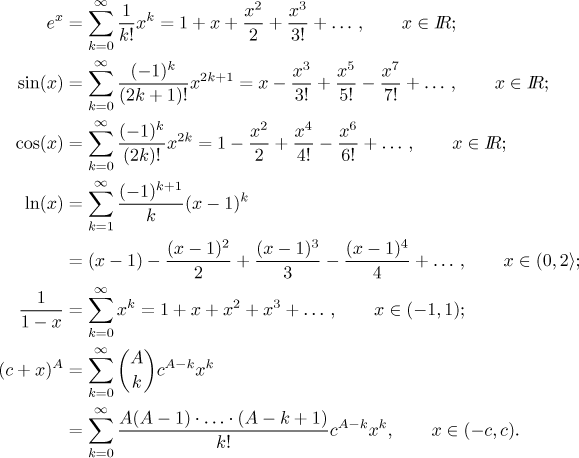
Równanie dla prawej części hiperboli o wzorze x² – y² = 1

Sinus hiperboliczny: $\sinh x=\frac{{{e}^{x}}-{{e}^{-x}}}{2}$

Cosinus hiperboliczny: $\cosh x=\frac{{{e}^{x}}+{{e}^{-x}}}{2}$

Tangens hiperboliczny: $tghx=\frac{\sinh x}{\cosh x}=\frac{{{e}^{x}}-{{e}^{-x}}}{{{e}^{x}}+{{e}^{-x}}}$

Kotangens hiperboliczny: $ctghx=\frac{\cosh x}{\sinh x}=\frac{{{e}^{x}}+{{e}^{-x}}}{{{e}^{x}}-{{e}^{-x}}}$

https://blog.etrapez.pl/funkcje-hiperboliczne/

${{\cosh }^{2}}x-{{\sinh }^{2}}x=1$ (podobne, ale nie takie same, to jest do jedynki trygonometrycznej)

$\cosh 2x={{\cosh }^{2}}x+{{\sinh }^{2}}x$ (podobnie do wzoru na cos2x)

$\sinh 2x=2\sinh x\cosh x$ (identycznie do wzoru na sinx)

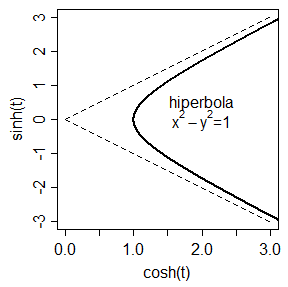
Hiperbola (stgr. ὑπερβολή hyperbolḗ „przerzucenie; przesada”^[1][2]) – krzywa będąca zbiorem takich punktów, dla których wartość bezwzględna różnicy odległości tych punktów od dwóch ustalonych punktów nazywanych ogniskami hiperboli jest stała.

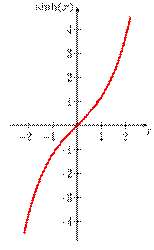
cosh(x)

Wykresy funkcji sinus, cosinus i tangens hiperboliczny

Wykresy funkcji cotangens, secans i cosecans hiperboliczny

Wreszcie przechodzimy już do tematu głównego

Liczby zespolone (Komlexní čísla)

Proszę najpierw zaznajomić się z podstawowymi informacjami o liczbach zespolonych1

Polecam bardzo zaznajomić się najpierw z bardzo przystępną formą objaśnienia w języku polskim wprowadzenia podstaw właściwości liczb zespolonych i podstawowych działań na nich, za pomocą nagrania w you tube punkt a). Proszę również zaznajomić się z obsługą tej aplikacji, gdzie można sobie ustawić wielkość zobrazowania, najlepiej na cały ekran, prędkość wykładu, najpierw z koeficjentem jeden (prędkość normalna), głośność dźwięku, i inne jeszcze parametry za pomocą ikonki kółka zębatego W razie potrzeby lepszego zrozumienia danej części wykładu można go zatrzymać i znów go kontynuować. Polecam wykład ten i dalej polecone nagrania prześledzić jeszcze kilka razy, np. z prędkością mniejszą 0,75 dla początkujących lub dla tych bardziej zaawansowanych, którzy powtarzają sobie już indziej nabyte wiadomości w tej dziedzinie matematyki, prędkością większą, np. 1,25.

a) https://www.youtube.com/watch?v=WuaBtDHWrv0 – liczby zespolone ogólnie.

Myśmy z braku czasu nie prześledzili tego wykładu do końca. Zaznajomiliśmy się z definicją liczby zespolonej, iż można ją zobrazować, np. w układzie współrzędnych kartezjańskich, gdzie na osi poziomej (oś odciętych, np. x) wyznacza się liczbą rzeczywistą część rzeczywistą liczby zespolonej, a na osi pionowej (oś rzędnych, np. y) wyznacza się również liczbą rzeczywistą pomnożoną przez jednostkę urojoną i (j). Obie te osie współrzędne wyznaczają na płaszczyźnie liczb zespolonych punkt, np. Z, który przedstawia liczbę zespoloną z. Oś x jest osią liczb rzeczywistych a oś y jest osią liczb urojonych.

https://encyklopedia.pwn.pl/haslo/wspolrzedne-kartezjanskie;3920788.html

Jednostka urojona i jest zdefiniowana w następujący sposób

(-1)^0,5= i albo lepiej i² = -1

Przy tej pierwszej definicji jednostki urojonej i możemy wpaść w pułapkę, której tutaj nie będę bliżej objaśniał. Poleca się używać tej drugiej definicji i² = -1

-1 = i²= (-1^1/2x (-1)^1/2 = (-1 x -1)^1/2 = 1

1/i = (1^1/2/(-1)^1/2 = (1/-1)^1/2 = (-1/1)^1/2 = (-1)^1/2 = i

Ważne! Przy rozwiązywaniu zadań nigdy nie zamieniaj symbolu i na (−1)^1/2, jeśli jest "i" to, niech tak zostanie, ale jeśli masz i², i³ itp. to już spokojnie możesz zastosować definicję i napisać i² = −1 lub np. i³ = i²x i = −1 x i = −i.

W pliku a) z nagrania you tube zaznajomiliśmy się z definicją płaszczyzny liczb zespolonych (płaszczyzny Arganda), z algebraiczną postacią liczby zespolonej, z dodawaniem, odejmowaniem, mnożeniem i dzieleniem liczb zespolonych właśnie w tej postaci. Dalej zaznajomiliśmy się z postacią trygonometryczną liczby zespolonej i tymi samymi działaniami matematycznymi w tej postaci. Dla łatwiejszego potęgowania i pierwiastkowania liczb zespolonych zaznajomiliśmy się z jej postacią, eksponencjalną (wykładniczą), z przykładem rozwiązywania liczby zespolonej, np. do potęgi 120. Ostatniego przykładu ze szczególnym zadaniem określenia części płaszczyzny liczb zespolonych już nie wykonaliśmy z powodu braku czasu.

Polecam przestudiować podane tutaj nagrania w you tube.

b) https://www.youtube.com/watch?v=MkG2NGBzKRU postać trygonometryczna.

c) https://www.edukator.pl/tik_edukator/Okrag_je funkcje na okręgu jednostkowym

d) https://cs.wikipedia.org/wiki/Euler%C5%AFv_vzorec, wzór Eulera.

e) https://www.matemaks.pl/wzor-de-moivre-a-potegowanie-liczb-zespolonych.html.

f) https://www.matemaks.pl/pierwiastkowanie-liczb-zespolonych.html.

g) https://www.youtube.com/watch?v=VK6WXlgosNk dělení komplex. č. v gon. tvaru

h) https://pl.wikipedia.org/wiki/Liczby_zespolone ładny wykład bez prezentacji filmowej!

https://www.youtube.com/watch?v=icqHFIdPaeY

https://www.youtube.com/watch?v=Gh6OPfuldlM

Na razie tyle

--------------------------------------------------------------------------

Kolejne przykłady do przestudiowania

5) https://www.matemaks.pl/pierwiastkowanie-liczb-zespolonych.html Wzór de Moivre'a - potęgowanie liczb zespolonych Moivrea

6 https://www.youtube.com/watch?v=jaorPYjbjSw

7) https://cs.wikipedia.org/wiki/Euler%C5%AFv_vzorec Eulerův vzorec

https://www.youtube.com/watch?v=WuaBtDHWrv0 l

8) https://www.youtube.com/watch?v=JS-i682gthA

9) https://pl.wikipedia.org/wiki/Liczby_zespolone

10) http://www.foton.if.uj.edu.pl/documents/12579485/cda7aaf1-8a00-4206-9498-07cd3142e543

11) https://pl.wikipedia.org/wiki/Pr%C4%85d_przemienny

12) https://www.edukator.pl/tik_edukator/Okrag_jednostkowy/index.html

13) https://www.youtube.com/watch?v=WuaBtDHWrv0

Dalej po podstawowym zapoznaniu się z liczbami zespolonymi!

Wzór de Moivre'a – potęgowanie liczb zespolonych

Liczby zespolone z,w∈C, z argumentami odpowiednio: α i β, możemy zapisać w postaci trygonometrycznej

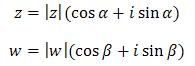
Obliczymy teraz iloczyn tych liczb zapisanych w postaci trygonometrycznej:

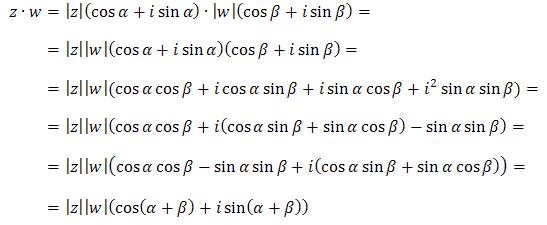
Ostatnia równość wynika ze wzorów trygonometrycznych na cosinus sumy kątów oraz na sinus sumy kątów. Powyższy rachunek pokazuje, że przy mnożeniu dwóch liczb zespolonych z, w∈C otrzymujemy liczbę zespoloną, której:

moduł jest iloczynem modułów liczb z oraz w,

argument jest sumą argumentów liczb z oraz w.

Wynika stąd następujący wzór:

Wzór de Moivre'a

Dla dowolnej liczby z∈C zachodzi następujący wzór:

Potęgowanie

Wzór do obliczenia n-tego pierwiastka z liczby zespolonej na

podstawie twierdzenia Moivrea

Pierwiastek liczby zespolonej , gdzie a różni się od zera i n jest liczbą całkowitą, potem istnieje właśnie n liczb zespolonych, które są n-tym pierwiastkiem z a, tzn. takich liczb z, że . Są to liczby

gdzie .

Tożsamość Eulera

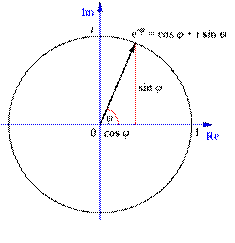
Euler's formula.svg

Dzielenie liczb zespolonych w postaci algebraicznej

https://www.youtube.com/watch?v=Lh91nkj7IXw

Dzielenie liczb zespolonych w postaci trygonometrycznej i wykładniczej

https://www.youtube.com/watch?v=LL7yq7JZMiI

Wzór ogólny na mnożenie i dzielenie liczb zespolonych w postaci trygonometrycznej

https://eszkola.pl/matematyka/dzialania-na-liczbach-zespolonych-w-postaci-trygonometrycznej-9810.html

Działania na liczbach zespolonych w postaci trygonometrycznej

Postać trygonometryczna liczby zespolonej umożliwia bardzo łatwe wykonywanie mnożenia i dzielenia liczb zespolonych. Wykonywanie tych działań na liczbach w postaci algebraicznej wymagało pewnego wysiłku, natomiast dysponując postacią trygonometryczną możemy to zrobić w prostszy sposób.

Niech dane będą dwie liczby w postaci trygonometrycznej:

$z_1=|z_1 |(\cos \alpha +i\sin \alpha )$ oraz $z_2=|z_2 |(\cos \beta +i\sin \beta )$ .