********************************************************************************************************************

Biuletyn Internetowy

Stowarzyszenia Elektrotechników Polskich

w Republice Czeskiej

BIULETYN SEP – numer 49

Czeski Cieszyn

12 / 2021 r.

http://www.coexistentia.cz/SEP/index.html

********************************************************************************************************************

Vysoká škola báňská – Technická univerzita w Ostrawie

Protokół ze zebrania członkowskiego SEP – 15.4.2021 r.

Zebranie odbyło się w czwartek 15.4.2021 r. w Czeskim Cieszynie w siedzibie firmy EMTEST sp. z o. o. Przyjęto następujący program obrad: a) zagajenie, b) sprawozdanie z działalności za 2020 rok, c) wybory zarządu SEP i komisji rewizyjnej SEP na 2021 rok, d) uchwalenie planu pracy na 2021 rok, e) uchwała. Przewodniczący SEP, Tadeusz Toman, poinformował, że w związku z informacją Ministerstwa Zdrowia Republiki Czeskiej o możliwości spotkań 10 osób, na zebranie zaproszono właśnie dziesięciu członków SEP. Jednak z powodu chaosu w epidemicznych rozporządzeniach rządowych – możliwość spotkań 10osobowych zmieniono na 2osobowe – udział w zebraniu wzięło czterech członków. Sprawozdanie z działalności na 2020 rok obecni otrzymali na piśmie. Uchwalono, że zarząd i komisja rewizyjna działać będą w niezmienionym składzie: przewodniczący – Tadeusz Toman, 1. zastępca przewodniczącego – Tadeusz Parzyk, 2. zastępca przewodniczącego – Tomasz Stopa, sekretarz – Stanisław Feber, księgowy – Zygmunt Stopa, komisja rewizyjna – Władysław Drong, Franciszek Jasiok, Władysław Niedoba. W związku z nienormalną sytuacją, kiedy rząd nie jest w stanie przedstawić perspektywy wznowienia działalności stowarzyszeń obywatelskich, uchwalono, że odbędą się dwa kameralne spotkania we wrześniu i grudniu. Każdy trzeci czwartek miesiąca będzie zapewniony dyżur w biurze. Przyjęto uchwałę następującej treści: SEP a) przyjmuje do wiadomości sprawozdanie z działalności SEP za 2020 rok, b) przyjmuje do wiadomości sprawozdanie kasowe SEP za rok 2020, c) wybiera zarząd SEP w składzie: Tadeusz Toman – przewodniczący, Tadeusz Parzyk – 1. zastępca przewodniczącego SEP, Tomasz Stopa – 2. zastępca przewodniczącego SEP, Stanisław Feber – sekretarz, Zygmunt Stopa – księgowy, d) wybiera komisję rewizyjną SEP w składzie Władysław Drong, Franciszek Jasiok, Władysław Niedoba, e) zobowiązuje przewodniczącego SEP poinformować bank – Poštovní spořitelna o zmianie siedziby SEP – niespełnione zadanie z poprzedniego zebrania, f) przyjmuje plan pracy SEP i budżet na 2021 rok, g) upoważnia przewodniczącego SEP zapewnić obecność w siedzibie SEP zawsze trzeci czwartek miesiąca w godz. 15:30-15:45, f) zobowiązuje zarząd SEP kontynuować współpracę z Oddziałem Gliwickim i Oddziałem Bielsko-Bialskim Stowarzyszenia Elektryków Polskich.

Spotkanie członkowskie SEP – 21.10.2021 r.

Spotkanie członków Stowarzyszenia Elektrotechników Polskich w Republice Czeskiej (SEP) odbyło się w czwartek 21.10.2021 r. o godz. 15:30 w Czeskim Cieszynie w siedzibie firmy EMTEST sp. z o. o. SEP liczy aktualnie 14 członków, w spotkaniu wzięło udział sześciu. Omawiano plan pracy na 2022 rok. Działalność uzależniona będzie od ograniczeń epidemicznych. Dyskutowano również o stanie kasy i sytuacji personalnej.

Spotkanie elektryków z prelekcją – 25.11.2021 r.

We czwartek 25.11.2021 r. odbyło się w salce konferencyjnej firmy EMTEST sp. z o. o. w Czeskim Cieszynie spotkanie członków Stowarzyszenia Elektrotechników Polskich w Republice Czeskiej (SEP), w ramach której prelekcję pt. „MATEMATYKA – NIEZBĘDNE NARZĘDZIE ELEKTROTECHNIKI“ wygłosił kol. inż. Bogusław Kaleta, CSc. Po zagajeniu i przywitaniu kolegów i gości, przez przewodniczącego SEP-u w RC, inż. Tadeusza Tomana, została rozpoczęta prelekcja Bogusława Kalety.

Bogusław Kaleta, jako aktywny amatorski korektor języka polskiego i czeskiego zaproponował zebranym, zaraz na początku prelekcji, w ramach krótkiej rozgrzewki, przybliżenie najbardziej rażących błędów językowych w języku polskim, których nasz przeciętny obywatel kierunku działań technicznych sam sobie wcale ich nie uświadamia! Ta rozgrzewka językowa okazała się przydatna. Ponieważ zaawansowanie w szerokiej dziedzinie elektrotechnicznej kolegów jest różnorodne, dlatego prelegent zaoferował obecnym powtórkę i poszerzenia wiedzy z podstaw matematyki aplikowanej w elektrotechnice, a mianowicie skierowanej na wykorzystanie liczb zespolonych w obliczeniach, na prostszych działaniach, którymi, można dobrze zastąpić bardziej złożony aparat matematyczny. Zaczął go objaśniać kolegom od najprostszych, ale najpotrzebniejszych działań w matematyce, tj. od charakterystyk rodzajów liczb – naturalnych, całkowitych, wymiernych, niewymiernych i rzeczywistych, powtórzył najważniejsze działania z algebry, a szczególnie zaznajomił ich z funkcjami trygonometrycznymi aż po liczby zespolone, ponieważ jako pedagog uniwersytecki z ponad 30-letnią praktyką na Uniwersytecie Żylińskim w Żylinie, Wydziale Elektrotechnicznym, Katedrze Systemów Sterowanych i Informatycznych, wiedział jak najlepiej przygotować swych kolegów do powtórki lub wprowadzenia ich do szerokiej dziedziny matematyki używanej w elektrotechnice, a mianowicie do działań matematycznych na liczbach zespolonych. Objaśnił im definicję liczby zespolonej, jej zobrazowanie na płaszczyźnie zespolonej, zapoznał ich bliżej z formami w jakich te liczby występują, tj. w postaci algebraicznej, trygonometrycznej i eksponencjalnej (wykładniczej). Zaznajomił ich za pomocą aplikacji filmowej z podstawowymi działaniami matematycznymi na liczbach zespolonych. Były to: dodawanie, odejmowanie, mnożenie, dzielenie, potęgowanie również w każdej ich postaci: algebraicznej, trygonometrycznej i eksponencjalnej. Z braku czasu nie został już pokazany interesujący przykład ograniczania płaszczyzny zespolonej przez różne parametry ją określające oraz pierwiastkowanie liczb zespolonych. Bogusław Kaleta polecił swym kolegom przerobić wskazane im tematy działań matematycznych na liczbach zespolonych, które w przystępny sposób objaśniają daną problematykę w języku polskim, a można je znaleźć w poleconych nagraniach filmowych. Niektóre z nich, chociaż mają bardzo zbliżoną nazwę nagrania filmowego objaśniają ten sam problem w inny sposób i na innym przykładzie. Można więc znaleźć jeszcze nieprzebrane pierwiastkowanie liczb zespolonych, logarytmowanie, różne postacie funkcji eksponencjalnych o podstawie liczby Eulera e, popatrzeć nie tylko na wskazywane wzory funkcji matematycznych, ale i na sposób ich wyprowadzania. Jeśli będzie zainteresowanie kolegów, to można kiedyś na przykładzie długiej linii elektrycznej, wyliczyć za pomocą równań telegrafistów, napięcie i prąd harmoniczny na początku linii elektrycznej z potrzebnego napięcia i prądu na jej końcu. Materiały prelekcji zostaną przesłane e-mailami członkom i sympatykom SEP-u oraz mogą być zamieszczone przez pana Władysława Dronga na stronach internetowych SEP-u.

Spotkanie kolegów elektrotechników i ich sympatyków zakończył Tadeusz Toman, podziękowaniem Bogusławowi Kalecie za opracowanie bogatego materiału do prelekcji i za jej przeprowadzenie. W związku z ograniczeniami epidemicznymi zadecydowano, że kolejne spotkanie – zebranie członkowskie, odbędzie się dopiero trzeci czwartek lutego 2022 roku.

VŠB-Technická univerzita: absolwenci o zatrudnienie w branży obawiać się nie muszą

Szkoły wyższe, przede wszystkim te typu uniwersyteckiego, nie tylko kształcą studentów. Są również żywym organizmem i ważną częścią składową życia regionów i miast, w których działają. W Województwie Morawsko-Śląskim jest kilka wysokiej jakości szkół wyższych. Proponują one różnorakie programy nauczania.

Najdłużej działa Vysoká škola báňská – Technická univerzita Ostrava (Wyższa Szkoła Górnicza – Uniwersytet Techniczny w Ostrawie). Specjalistów dla podstawowych gałęzi przemysłu przygotowują tu już przeszło 170 lat. Szkoła w początkach swego istnienia koncentrowała się na dwie dziedziny pierwszej rewolucji przemysłowej – na wydobycie węgla i produkcję stali, ale z biegiem lat dołączyły kolejne dziedziny, które w czasie jej powstania jeszcze nie istniały. Dziś na siedmiu fakultetach można studiować nowoczesne kierunki takie, jak technologia i informatyka, energia alternatywna, architektura lub ekonomika.

Natomiast Ostravská univerzita (Uniwersytet Ostrawski) jest jedną z najmłodszych szkół wyższych w Republice Czeskiej. W bieżącym roku obchodzi trzydziestą rocznicę istnienia. Od 1991 roku, kiedy posiadała trzy fakultety, poszerzyła się o kolejne trzy. Kształci studentów przede wszystkim w kierunkach nauk przyrodniczych i socjalnych. Obecnie na brzegu rzeki Ostrawicy powstaje kampus, gdzie będą mogli przychodzić nie tylko studenci, ale również mieszkańcy Ostrawy za wiedzą i zabawą.

Również Slezská univerzita Opava (Uniwersytet Śląski w Opawie) obchodzi w bieżącym roku okrągłą rocznicę powstania. Uniwersytet założono przed trzydziestu laty i stał się ważną częścią składową regionu. Obecnie posiada trzy fakultety w Opawie i jeden fakultet w Karwinie. Pomimo, że kształci niespełna 5000 studentów, proponuje niemal sto kierunków studyjnych i organizuje szereg kursów w ramach kształcenia całego życia Uniwersytetu Trzeciego Wieku.

W Województwie Morawsko-Śląskim istnieją również prywatne szkoły wyższe. Jedną z nich jest Vysoká škola podnikání a práva (Wyższa Szkola Przedsiębiorczości i Prawa) z więcej niż dwudziestoletnią historią. Szkoła działa również w Brnie i Pradze i ma ambicję należeć do najlepszych instytucji kształcących przyszłych przedsiębiorców i pracowników środowisk przemysłowych w regionie.

Dlaczego młodzi ludzie mają wybierać studia w Wyższej Szkole Górniczej – Uniwersytecie Technicznym w Ostrawie? Powód jest stosunkowo prosty. O ile młodzi ludzie chcą rozumnie nastartować swoją karierę zawodową, wybierają perspektywiczną dziedzinę z pewnym wykorzystaniem swoich kwalifikacji. Zaletą absolwentów szkoły jest bezsprzecznie, że niemal wszyscy są zatrudnieni zgodnie ze swoim wykształceniem i są dobrze wynagradzani. Widać to przede wszystkim w wielkich zakładach przemysłowych w regionie, gdzie większość pracowników na kierowniczych stanowiskach to absolwenci szkoły. Firmy nieustannie dopytują się o studentów szkoły i to jest kolejnym dowodem na to, że studium jest tak postawione, że odpowiada praktycznym potrzebom. Jakie są nowe, atrakcyjne dziedziny kształcenia w szkole? Unikatowy jest Desing przemysłowy, interesująco koncypowany między Wyższą Szkołę Górniczą – Uniwersytet Techniczny w Ostrawie i Uniwersytet Palackiego w Ołomuńcu. Kształci szczytowych desyngerów z jakościowymi znajomościami technicznymi, które można wykorzystać w wielu dziedzinach desingu – od przemysłu samochodowego przez 3D grafikę i modelarstwo aż po projekty interierów. Wyjątkowe jest Odlewnictwo artystyczne, program studyjny pomiędzy techniką i sztuką i oczywiście programy Fakultetu górniczo-geologicznego ukierunkowane na wydobycie i rewitalizację krainy, czy wodę jako surowiec strategiczny. Szkoła proponuje dziesiątki programów studyjnych, dlatego urozmaicone są również możliwości zatrudnienia absolwentów szkoły. W jaki sposób szkoła uczestniczy w życiu miasta czy województwa, w którym działa? Z kierownictwem miasta i województwa, które szkołę długofalowo popierają, uzgodnione są priorytety. To, co w regionie trzeba w przyszłości zasadniczo zmienić, to wytworzyć dla młodych, zdolnych ludzi takie warunki, aby chcieli tu nie tylko pozostać, ale również prowadzić przedsiębiorstwa, dlatego konieczne jest wspólnie szukać możliwości, jak takich ludzi przywabić do regionu. Obecnie są przygotowywane nowe projekty europejskie, przykładowo wspólny projekt o nazwie Global experts, ukierunkowany na szczytowych naukowców. Jeśli uda się nastartować ich działalność tu w regionie, będą wokół nich w sposób naturalny powstawać zespoły miejscowych fachowców. Uniwersytet uczestniczy również w szerokiej skali działalności, które mają związek z życiem obywateli miasta i województwa. Nie jest łatwo wybrać tylko niektóre, ale ocena, również na poziomie narodowym, za odpowiedzialność społeczną jest tego potwierdzeniem. Trzecia rola uniwersytetu jest po prostu naturalną częścią składową jego aktywności. VŠB – technická univerzita jest motorem napędowym przemian regionu z województwa ukierunkowanego na wydobycie węgla i przemysł hutniczy na województwo IT, przemysłu maszynowego, budownictwa i nowoczesnych technologii czy bezpieczeństwa.

Przeczytaliśmy: Oszczędzamy, aby płacić (trochę) mniej

Rachunki za energię elektryczną i gaz spędzają sen z powiek nie tylko Czechom i Polakom, ale też obywatelom większości krajów Unii Europejskiej. Ceny idą w górę i nic nie wskazuje na to, że w najbliższych miesiącach miałoby być lepiej. Dodatkowym problemem są upadłości firm energetycznych – ich klienci muszą się liczyć z dodatkowymi kosztami związanym ze zmianą dostawcy energii. Skoro zatem groźba coraz wyższych opłat za prąd i gaz wisi nad nami niczym miecz Damoklesa, warto zrobić wszystko, aby ograniczyć zużycie bez większych i bolesnych wyrzeczeń.

Jeżeli ogrzewamy mieszkanie prądem lub gazem, powinniśmy pamiętać, że obniżając w pomieszczeniu temperaturę o jeden stopień Celsjusza, oszczędzamy nawet 6 proc. energii. Temperatura w kuchni i pokoju gościnnym powinna wynosić ok. 20^O C, w sypialni o dwa stopnie mniej, łazienkę zaś warto ogrzać do 24^O C, a pokój dziecinny do 22^O C. Ważne jest uszczelnienie okien i drzwi, ale z termoizolacją pomieszczeń mieszkalnych nie należy mimo wszystko przesadzać. Mieszkanie powinno być (krótko, lecz intensywnie) wietrzone (wystarczy kilka czy kilkanaście minut, w zależności od temperatury na zewnątrz), a okna uszczelnione i wyposażone w nawiewniki. Kaloryferów nie należy zasłaniać dużymi meblami ani zasłonami, aby ciepło bez przeszkód mogło płynąć do mieszkania.

Zużycie gazu i prądu można ograniczyć, używając do podgrzewania potraw naczyń o niezbyt grubych ścianach, zaś do dłuższego gotowania – naczyń o grubszych ścianach, posiadających dno akumulacyjne. Średnica garnka musi być trochę większa od korony palnika. Jeżeli to możliwe, należy gotować pod przykryciem, można bowiem w ten sposób zaoszczędzić nawet 50 proc. gazu i prądu. W trakcie pieczenia otwieramy piekarnik jak najrzadziej. Przed pieczeniem (gotowaniem) należy żywność rozmrozić. O tym, że lodówki nigdy nie należy ustawiać w bezpośrednim sąsiedztwie kuchenki, piekarnika, czy kaloryferów, nie trzeba nikomu przypominać. Warto też dopilnować, aby wnętrze lodówki nie było zbyt oblodzone, ponieważ wtedy pobór mocy jest o wiele większy. Nigdy nie wkładamy do lodówki gorących lub ciepłych potraw. No i nie otwieramy lodówki bez potrzeby. W czajniku bezprzewodowym należy zawsze zagotować tylko tyle wody, ile będziemy potrzebować. Zarówno ze zmywarki, jak i z pralki trzeba korzystać tylko wtedy, gdy są wypełnione. Nowszy sprzęt umożliwia korzystanie z trybu „eko“ lub specjalnego programu energooszczędnego.

Spróbujmy jak najwięcej korzystać ze światła dziennego. Czasami warto biurko przenieść bliżej okna. Żaluzje i zasłony to świetna rzecz, ale nie powinny zmuszać nas do zapalania światła w pokoju wtedy, gdy za oknem panuje słoneczna pogoda. Energooszczędne żarówki to dzisiaj w naszych domach oczywistość. Dla przykładu – żarówki LED pozwalają zaoszczędzić nawet 80 proc. energii przy pięciokrotnym zwiększeniu efektywności świetnej. Ich żywotność jest dłuższa, aniżeli żywotność tradycyjnych żarówek (wynosi nawet 25 tys. godzin). Kiedy opuszczamy pomieszczenie, LED żarówki możemy bez obaw wyłączyć. Tzw. świetlówki kompaktowe częstego włączania i wyłączania jednak raczej nie lubią – przerwa w ich eksploatacji powinna wynosić co najmniej 30 minut, w przeciwnym wypadku łatwo się psują. Jeżeli oświetlamy także okolicę domu, warto pomyśleć o skorzystaniu z czujnika ruchu. Wtedy światło włączać będzie się tylko wówczas, gdy jest to konieczne, np. wtedy, gdy ktoś stanie pod drzwiami.

Warto wiedzieć, że ładowarka podłączona do kontaktu i do naładowanego już urządzenia dalej zużywa prąd. Na koniec warto przypomnieć, że tzw. tryb czuwania (stand-by) to też niemały pożeracz prądu elektrycznego. Jest jednak wygodny, gdyż pozwala na uruchomienie komputera czy telewizora szybko i w dowolnym momencie. Jeżeli możemy z niego zrezygnować, zaoszczędzimy ok. 2 tys. koron rocznie. Kwota nie powala co prawda na kolana, ale jak mówi przysłowie – ziarnko do ziarnka, a zbierze się miarka. A owa miarka w sytuacji, gdy trudno przewidzieć, ile przyjdzie nam płacić za energie za kilka miesięcy czy za rok, na pewno ma swoje znaczenie.

(„Głos“ – gazeta Polaków w Republice Czeskiej, 9.11.2021 r.)

„Matematyka – niezbędne narzędzie elektrotechniki“

Systemy liczbowe (Číselné systémy)

System liczbowy – zbiór (množina) reguł jednolitego zapisu i nazewnictwa liczb. Do zapisywania liczb używa się skończonego zbioru znaków, zwanych cyframi, które można łączyć w dowolnie długie ciągi, otrzymując nieskończoną liczbę kombinacji.

Cyfra, liczba, ilość (číslice, číslo, množství)

Cyfra jest znakiem graficznym. Cyfr arabskich jest dziesięć: 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9,

a dziś używanych rzymskich siedem: I, V, X, L, C, D, M.*

Liczba oznacza "stan liczebny" albo pojęcie, którego treścią jest wynik liczenia wyrażony zwykle cyframi. Liczba odnosi się więc do rzeczy "policzalnych", przedmiotów (żywych i martwych), które można kolejno policzyć. Ilość jest miarą tego, co może być mierzone lub ważone, to jest odnosi się do rzeczy "niepoliczalnych", np. gazów, cieczy, ciał sypkich, pojęć abstrakcyjnych itp.

Należy pisać: liczba ludzi, liczba pomysłów, liczba krwinek płytkowych, liczba książek. Ilość mąki, ilość powietrza, ilość białka, ilość rozumu.

Nie należy używać: ilość ludzi, cyfra dwadzieścia trzy (to dwie cyfry!)

Rodzaje liczb (Druhy čísel)

Liczby naturalne (Přírozená čísla)

Liczby naturalne – to liczby całkowite, dodatnie: 1,2,3,4,5,6, …

Czasami do liczb naturalnych zaliczamy również liczbę zero (autor książki matematycznej powinien zawsze jasno określić, czy uznaje liczbę zero za naturalną, czy też nie!).

Zbiór (mnogość elementów, pojęcie pierwotne, aksjomat) liczb naturalnych oznaczamy literą N.
Możemy zapisać, że:

N = {1,2,3,4,5,6, …}

Jeżeli zakładamy, że zero również jest liczbą naturalną, to zapiszemy:

N = {0,1,2,3,4,5, …}

Czasami dla zbioru liczb naturalnych dodatnich stosujemy oznaczenie N+.

N+ = {1,2,3,4,5,6, …}

Ten sam zbiór możemy również zapisać wykorzystując symbol liczb całkowitych:

Z+ = {1,2,3,4,5,6, …}

(nawiasy okrągłe, kwadratowe, klamrowe, ostrokątne)

Liczby całkowite (Celá čísla)

Liczby całkowite ─ to liczby naturalne oraz ich ujemne odpowiedniki, a także liczba zero:

… −6,−5,−4,−3,−2,−1, 0, 1, 2, 3, 4, 5, 6, ….

Zbiór liczb całkowitych oznaczamy symbolem Z.

Z = {… −6,−5,−4,−3,−2,−1, 0, 1, 2, 3, 4, 5, 6, …}

Zbiór liczb całkowitych dodatnich to:

Z+ = {1, 2, 3, 4, 5, 6, …}

Możemy także zapisać zbiór liczb całkowitych ujemnych:

Z− = {… −6,−5,−4,−3,−2,−1}, z niemieckiego ganze Zahlen

Zbiór liczb całkowitych dodatnich, to zbiór liczb naturalnych.

Liczby wymierne (Racionální čísla)

Liczba wymierna – to taka liczba, którą można zapisać w postaci ułamka zwykłego, czyli w postaci:

p/q

gdzie: p – to dowolna liczba całkowita

q – to liczba całkowita różna od 0 (ponieważ nie wolno dzielić przez zero!).

Zbiór liczb wymiernych oznaczamy symbolem Q.

Formalnie zbiór liczb wymiernych można zapisać w taki sposób:

Q = {p/q:p,q∈Z⊥q≠0}

Przykład 1.

Liczba 3/4 jest wymierna, ponieważ jest zapisana w postaci ułamka zwykłego.

Twierdzenie 1. Każda liczba całkowita jest wymierna.

Każdą liczbę wymierną można zapisać za pomocą ułamka na dowolnie wiele sposobów.

Przykład 2.

Liczba 1 jest wymierna, ponieważ można ją zapisać w postaci ułamka zwykłego:

1/1 = 4/4 = 11/11 = 4/4 = 17/17 = 1

Przykład 3.

Liczba 5 jest wymierna, ponieważ można ją zapisać w postaci ułamka zwykłego:

5/1 = 10/2 = 60/12 = 5:1 = 5

Przykład 4.

Liczba −3 jest wymierna, ponieważ można ją zapisać w postaci ułamka zwykłego:

−3/1 =−6/2 = 900/300 = 3

Przykład 5.

Liczba 0 jest wymierna, ponieważ można ją zapisać w postaci ułamka zwykłego:

0/1 = 0/2 = 0/3 = 0

Przykład 6.

Liczba 17/8 jest wymierna, ponieważ można ją zapisać w postaci ułamka zwykłego:

17/8 = 15:8

Przykład 7.

Liczba 0,(3) jest wymierna, ponieważ można ją zapisać w postaci ułamka zwykłego:

0,(3) = 1/3 = 0,33333 (okres 3)

Przykład 8.

Liczba 4^1/2jest wymierna, ponieważ można ją zapisać w postaci ułamka zwykłego:

4^1/2 = 2 = 2/1

Przykład 9.

Liczba 125^1/3 jest wymierna, ponieważ można ją zapisać w postaci ułamka zwykłego:

125^1/3 = 5 = 5:1

Liczba w liczniku ułamka wykładnika oznacza stopień potęgi,

w mianowniku oznacza stopień pierwiastka!

Liczby niewymierne (Iracionální čísla)

Liczba niewymierna to taka liczba, której nie można zapisać za pomocą ułamka zwykłego.

Przykład 1.

(x^5/3) = to są dwa sposoby zapisów identycznych

Liczbami niewymiernymi są np.:

2^1/2, 3^1/2, 5^1/2, 17^1/2, 2^1/3, π, e …

Żadnej z tych liczb nie da się zapisać w postaci ułamka zwykłego!

Liczba Ludolfa π = 3,14159265359 …,

Liczba Eulera e = 2,71828182845904523536028747135266249775724709.

Uwaga! Nie każdy pierwiastek jest liczbą niewymierną, np.:

9^1/2 = 3 = 3/1

Suma liczby wymiernej i niewymiernej jest zawsze liczbą niewymierną!

Iloczyn (mnożenie) dwóch liczb niewymiernych może być liczbą wymierną albo niewymierną!

liczba 2^1/2. 2^1/2 = 4^1/2=2 jest wymierna

2^1/2 .3^1/2= 6^1/2 niewymierna

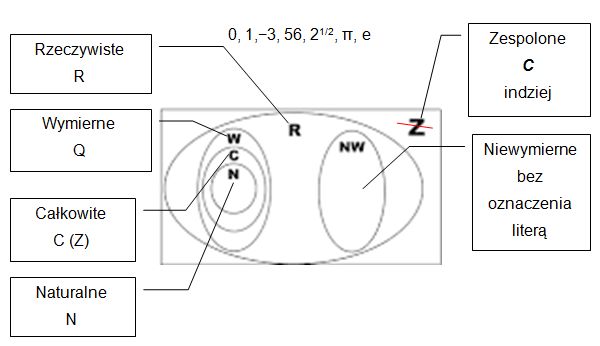
Liczby rzeczywiste (Reálná čísla)

Liczby niewymierne wraz z liczbami wymiernymi tworzą zbiór liczb rzeczywistych.

Zbiór liczb rzeczywistych oznaczamy symbolem R

Liczbami rzeczywistymi są, np.:

Potęgi:

Przykłady:

Pierwiastki

Przykłady:

Definicje funkcji trygonometrycznych kąta ostrego – metoda graficzna do zapamiętania

Aby obliczyć sinus kąta ostrego w trójkącie prostokątnym (v pravoúhlém trojúhelníku), to:

patrzymy najpierw na bok naprzeciwko kąta,

potem na przeciwprostokątną.

Aby obliczyć cosinus kąta ostrego w trójkącie prostokątnym, to:

patrzymy najpierw na przyprostokątną przy kącie,

Aby obliczyć tangens kąta ostrego w trójkącie prostokątnym, to:

patrzymy najpierw na bok naprzeciwko kąta,

potem na drugą przyprostokątną.

Aby obliczyć cotangens kąta ostrego w trójkącie prostokątnym, to:

patrzymy najpierw na przyprostokątną przy kącie,

potem na drugą przyprostokątną.

Zależności między funkcjami trygonometrycznymi kątów ostrych w trójkącie prostokątnym

Twierdzenie 1. Funkcje trygonometryczne kąta ostrego w trójkącie prostokątnym są dodatnie.
Uzasadnienie:

Funkcje trygonometryczne kątów ostrych w trójkącie prostokątnym obliczamy jako stosunki odpowiednich boków danego trójkąta. Boki trójkąta mają zawsze długość dodatnią, zatem ich stosunki również są dodatnie.

Twierdzenie 2. Tangens i cotangens są swoimi odwrotnościami, czyli:

ctgα = 1/tgα

albo inaczej:

tgα⋅ctgα = 1

Twierdzenie 3. Dla trójkąta prostokątnego:

[obrazek - fakt 3]

mamy:

sinα = cosβ

cosα = sinβ

tgα = ctgβ

ctgα = tgβ

Uzasadnienie:

Korzystając bezpośrednio z definicji funkcji trygonometrycznych otrzymujemy:

sinα = a/c cosα = b/c

tgα = a/b ctgα = b/a

oraz

sinβ = b/c cosβ = a/c

tgβ = b/a ctgβ = a/b

Zatem mamy:

sinα = a/c = cosβ

cosα = b/c = sinβ

tgα = a/b = ctgβ

ctgα = b/a = tgβ

Twierdzenie 4. W trójkącie prostokątnym:

[obrazek - fakt 4]

mamy:

β = 90°−α

Zatem:

sinα = cos(90°–α)

cosα = sin(90°−α)

tgα = ctg(90°−α)

ctgα = tg(90°−α)

Powyższe wzory to są tzw. wzory redukcyjne dla kąta 90°–α. Otrzymaliśmy je bezpośrednio z równości podanych w Twierdzeniu 3.

Okrąg jednostkowy (jednotková kružnice), o promieniu r = 1

Na tym okręgu jednostkowym o promieniu 1 można zobaczyć dużą liczbę jego własności: funkcje sinus, cosinus, tangens, cotangens, arcsin, arccosinus, sekans, kosekans …, funkcje miar łukowych (arcus) oraz już bardzo mało używane funkcje, jak np. versinx = (1 – cosx). Miara łukowa kąta była wprowadzona w 1714 roku, o wiele później niż miara kątowa w stopniach (w starej Babilonii (1792–1750 p.n.e.), różnica 3 506 lat.

Równanie okręgu jednostkowego

x² + y² = 1

Miara kąta – wielkość kąta wyrażona w odpowiednich jednostkach. W matematyce i jej zastosowaniach teoretycznych używa się miary łukowej.

Jest to długość łuku wyciętego przez kąt z okręgu o promieniu 1 i środku w wierzchołku kąta. Tak określona miara wyraża się liczbą niemianowaną (bezwymiarową) i może przyjmować wartości z zakresu 0 do 2π. Jednostkę miary łukowej nazywamy radianem.

Kąt α ma miarę 1 radiana, jeśli długość łuku równa jest promieniowi R.

https://upload.wikimedia.org/wikipedia/commons/4/4e/Circle_radians.gif

W życiu codziennym używa się zwykle miary stopniowej. Kąt pełny dzieli się na 360 stopni kątowych (symbol: °), każdy z nich na 60 minut kątowych (symbol: ′), a każdą z nich na 60 sekund kątowych (symbol: ″). Ułamki sekund kątowych podawane są już dziesiętnie.

Tę właśnie miarę wykorzystuje się w popularnych kątomierzach.

W praktyce militarnej i geodezyjnej stosowany bywa podział kąta pełnego na 400 gradów (lub gradusów, symbol: ^g), z których każdy dzieli się na 100 centygradów (symbol: ^c), a każdy z nich na 100 myriogradów (symbol: ^cc). Podział taki ułatwia ręczne (pisemne) dodawanie i odejmowanie, ponieważ przeniesienia i pożyczki wykonuje się jak przy zwykłych liczbach dziesiętnych, bez konieczności przeliczania na 60 i 90 jednostek.

W pomiarach nachylenia nawierzchni

Kąt	Tangens	Sinus
0°	0 %	0 %
5°	9 %	9 %
10°	18 %	17 %
30°	58 %	50 %
45°	100 %	71 %
60°	173 %	87 %
90°	∞	100

używa się miary procentowej (np. przy określeniu nachylenia nawierzchni drogi). Przykładowo 1% (w języku polskim znak procentu % stawia się zaraz obok liczby!)

1 procent oznacza zmianę wysokości o 1 cm na 100 cm długości.

Miara kąta potocznie nazywana jest kątem.

Zamiana stopni na radiany i odwrotnie radiany na stopnie

Stopnie możemy bardzo łatwo zamieniać na radiany za pomocą proporcji. Wystarczy, że pamiętamy, np. zależność: 360° = 2π (rad).

Przykład 1.

Wyraź za pomocą radianów kąt o mierze 60°

Rozwiązanie:

Układamy proporcję:

360° = 2π (rad)

60° = x (rad)

x(rad)/2π = 60°/360°

x = 2π 60/360

x(rad) = 2 razy. 3,14 60/360 = 1,046666 rad

x(rad) = 1,046666 rad

1 radian =360°/2π ≈ 57°

Dokładnie 1 radian = 57·17′45′′

deg = rad⋅180/π.

rad = deg.π/180

Radiany możemy zamieniać na stopnie za pomocą proporcji.

Wystarczy, że pamiętamy np. zależność: 360° = 2π (rad)

Wyraź za pomocą stopni kąt o mierze łukowej (π/5).

x° = π/5x360/6,28 = 3,14/5x360/6,28 = 36°

x° = (rad) 360/2π

deg = rad⋅180/π

Wykresy funkcji trygonometrycznych oraz wzory trygonometryczne

Rozwiązania podstawowych równań trygonometrycznych, liczba (Z)

Funkcje trygonometryczne kąta ostrego

Funkcje trygonometryczne kąta ostrego

Wartości funkcji trygonometrycznych wybranych kątów ostrych

Funkcje trygonometryczne dowolnego kąta (skierowanego – orientovaného)

Funkcje trygonometryczne dowolnego kąta (skierowanego)

Własności funkcji trygonometrycznych miara główna

Funkcja	Własność	Warunek	Dziedzina
	nieparzysta
	parzysta
	nieparzysta
	nieparzysta

Okresowość funkcji trygonometrycznych, liczba (Z)


Funkcja	Okres podstawowy	Warunek

Jedynki trygonometryczne

Związki między funkcjami trygonometrycznymi

Wzory redukcyjne, Liczba

Funkcje trygonometryczne sumy i różnicy kątów

Funkcje trygonometryczne kąta podwojonego

Funkcje trygonometryczne kąta potrojonego

Suma i różnica takich samych funkcji trygonometrycznych

Funkcje trygonometryczne połowy kąta

Funkcje trygonometryczne wyrażone przez tangens połowy kąta

Związki między funkcjami cyklometrycznymi

Dla	Dla


Dla	Dla

Trójkąt ogólny

Kąt zewnętrzny trójkąta

Kąt zewnętrzny a kąt wewnętrzny

Kąt zewnętrzny jako suma kątów wewnętrznych

katy w trójkącie, kąt zewnętrzny i wewnętrzny

suma kątów wewnętrznych w trójkacie

dwusieczne

Obrazek ten jest wadliwy!

Związki miarowe w trójkącie

związki miarowe w trójkącie

Twierdzenie sinusów (Snelliusa)	Twierdzenie kosinusów (Carnota)

Proszę o dokładne prześledzenie przebiegu funkcji trygonometrycznych

sinusa, cosinusa, tangensa i cotangensa

w zależności od miary kąta, na okręgu jednostkowym.

W edukatorze, proszę sobie wybrać sukcesywnie jedną

z czterech funkcji trygonometrycznych i uchwytem z kółkiem kręcić

i śledzić ich przebieg

https://www.edukator.pl/tik_edukator/Okrag_jednostkowy/index.html

Proszę zaznajomić się również z symbolami i znaczeniami matematycznymi w języku czeskim.

https://cs.wikipedia.org/wiki/Matematick%C3%A9_symboly_a_zna%C4%8Dky

i polskim oraz ubogacić swoją terminologię matematyczną w obu językach.

https://pl.wikipedia.org/wiki/Lista_symboli_matematycznych

Niektóre funkcje trygonometryczne wyrażone za pomocą szeregu Taylora

$\begin{align}\sin x &= x - \tfrac{x^3}{3!} + \tfrac{x^5}{5!} - \tfrac{x^7}{7!} + \cdots =\\&=\sum_{n=0}^\infty (-1)^n\tfrac{x^{2n+1}}{(2n+1)!}\\\cos x &= 1 - \tfrac{x^2}{2!} + \tfrac{x^4}{4!} - \tfrac{x^6}{6!} + \cdots =\\&=\sum_{n=0}^\infty(-1)^n\tfrac{x^{2n}}{(2n)!}\\\mbox{tg}\ x &= x + \tfrac{x^3}{3} + \tfrac{2 x^5}{15} + \cdots =\\&=\sum^{\infin}_{n=1} \tfrac{B_{2n} (-4)^n (1-4^n)}{(2n)!} x^{2n-1},\quad |x|<\tfrac{\pi}{2}\end{align}$

gdzie $B_n\;$ to liczby Bernoulliego

$\begin{align}\mbox{ctg}\ x&= \tfrac {1} {x} - \tfrac {x}{3} - \tfrac {x^3} {45} - \tfrac {2 x^5} {945} - \cdots =\\&=\sum_{n=0}^\infty \tfrac{(-1)^n 2^{2n} B_{2n} x^{2n-1}}{(2n)!},\quad 0 < |x| < \pi\\\sec x &= 1 + \tfrac {x^2} {2} + \tfrac {5 x^4} {24} + \tfrac {61 x^6} {720} + \cdots =\\&=\sum^{\infin}_{n=0} \tfrac{(-1)^n E_{2n}}{(2n)!} x^{2n},\quad |x|< \tfrac{\pi}{2}\end{align}$

gdzie $E_n\;$ to liczby Eulera

Funkcje hiperboliczne (Hyporbolické funkce)

Funkcje hiperboliczne to funkcje, których wartości powstają poprzez różne kombinowanie z wartościami funkcji , a konkretnie:

Równanie dla prawej części hiperboli o wzorze x² – y² = 1

Sinus hiperboliczny: $\sinh x=\frac{{{e}^{x}}-{{e}^{-x}}}{2}$

Cosinus hiperboliczny: $\cosh x=\frac{{{e}^{x}}+{{e}^{-x}}}{2}$

Tangens hiperboliczny: $tghx=\frac{\sinh x}{\cosh x}=\frac{{{e}^{x}}-{{e}^{-x}}}{{{e}^{x}}+{{e}^{-x}}}$

Kotangens hiperboliczny: $ctghx=\frac{\cosh x}{\sinh x}=\frac{{{e}^{x}}+{{e}^{-x}}}{{{e}^{x}}-{{e}^{-x}}}$

https://blog.etrapez.pl/funkcje-hiperboliczne/

${{\cosh }^{2}}x-{{\sinh }^{2}}x=1$ (podobne, ale nie takie same, to jest do jedynki trygonometrycznej)

$\cosh 2x={{\cosh }^{2}}x+{{\sinh }^{2}}x$ (podobnie do wzoru na cos2x)

$\sinh 2x=2\sinh x\cosh x$ (identycznie do wzoru na sinx)

Hiperbola (stgr. ὑπερβολή hyperbolḗ „przerzucenie; przesada”^[1][2]) – krzywa będąca zbiorem takich punktów, dla których wartość bezwzględna różnicy odległości tych punktów od dwóch ustalonych punktów nazywanych ogniskami hiperboli jest stała.

cosh(x)

Wykresy funkcji sinus, cosinus i tangens hiperboliczny

Wykresy funkcji cotangens, secans i cosecans hiperboliczny

Wreszcie przechodzimy już do tematu głównego

Liczby zespolone (Komlexní čísla)

Proszę najpierw zaznajomić się z podstawowymi informacjami o liczbach zespolonych

Polecam bardzo zaznajomić się najpierw z bardzo przystępną formą objaśnienia w języku polskim wprowadzenia podstaw właściwości liczb zespolonych i podstawowych działań na nich, za pomocą nagrania w you tube punkt a). Proszę również zaznajomić się z obsługą tej aplikacji, gdzie można sobie ustawić wielkość zobrazowania, najlepiej na cały ekran, prędkość wykładu, najpierw z koeficientem jeden (prędkość normalna), głośność dźwięku, i inne jeszcze parametry za pomocą ikonki kółka zębatego W razie potrzeby lepszego zrozumienia danej części wykładu można go zatrzymać i znów go kontynuować. Polecam wykład ten i dalej polecone nagrania prześledzić jeszcze kilka razy, np. z prędkością mniejszą 0,75 dla początkujących lub dla tych bardziej zaawansowanych, którzy powtarzają sobie już indziej nabyte wiadomości w tej dziedzinie matematyki, prędkością większą, np. 1,25.

https://www.youtube.com/watch?v=WuaBtDHWrv0 – liczby zespolone ogólnie.

Myśmy z braku czasu nie prześledzili tego wykładu do końca. Zaznajomiliśmy się z definicją liczby zespolonej, iż można ją zobrazować, np. w układzie współrzędnych kartezjańskich, gdzie na osi poziomej (oś odciętych, np. x) wyznacza się liczbą rzeczywistą część rzeczywistą liczby zespolonej, a na osi pionowej (oś rzędnych, np. y) wyznacza się również liczbą rzeczywistą pomnożoną przez jednostkę urojoną i (j). Obie te osie współrzędne wyznaczają na płaszczyźnie liczb zespolonych punkt, np. Z, który przedstawia liczbę zespoloną z. Oś x jest osią liczb rzeczywistych a oś y jest osią liczb urojonych.

https://encyklopedia.pwn.pl/haslo/wspolrzedne-kartezjanskie;3920788.html

Jednostka urojona i jest zdefiniowana w następujący sposób

(-1)^0,5= i albo lepiej i² = -1

Przy tej pierwszej definicji jednostki urojonej i możemy wpaść w pułapkę, której tutaj nie będę bliżej objaśniał. Poleca się używać tej drugiej definicji i² = -1

-1 = i²= (-1^1/2x (-1)^1/2 = (-1 x -1)^1/2 = 1

1/i = (1^1/2/(-1)^1/2 = (1/-1)^1/2 = (-1/1)^1/2 = (-1)^1/2 = i

Ważne! Przy rozwiązywaniu zadań nigdy nie zamieniaj symbolu i na (−1)^1/2, jeśli jest "i" to, niech tak zostanie, ale jeśli masz i², i³ itp. to już spokojnie możesz zastosować definicję i napisać i² = −1 lub np. i³ = i²x i = −1 x i = −i.

W pliku a) z nagrania you tube zaznajomiliśmy się z definicją płaszczyzny liczb zespolonych (płaszczyzny Arganda), z algebraiczną postacią liczby zespolonej, z dodawaniem, odejmowaniem, mnożeniem i dzieleniem liczb zespolonych właśnie w tej postaci. Dalej zaznajomiliśmy się z postacią trygonometryczną liczby zespolonej i tymi samymi działaniami matematycznymi w tej postaci. Dla łatwiejszego potęgowania i pierwiastkowania liczb zespolonych zaznajomiliśmy się z jej postacią, eksponencjalną (wykładniczą), z przykładem rozwiązywania liczby zespolonej, np. do potęgi 120. Ostatniego przykładu ze szczególnym zadaniem określenia części płaszczyzny liczb zespolonych już nie wykonaliśmy z powodu braku czasu.

Polecam przestudiować podane tutaj nagrania w you tube.

b) https://www.youtube.com/watch?v=MkG2NGBzKRU postać trygonometryczna.

c) https://www.edukator.pl/tik_edukator/Okrag_je funkcje na okręgu jednostkowym

d) https://cs.wikipedia.org/wiki/Euler%C5%AFv_vzorec, wzór Eulera.

e) https://www.matemaks.pl/wzor-de-moivre-a-potegowanie-liczb-zespolonych.html.

f) https://www.matemaks.pl/pierwiastkowanie-liczb-zespolonych.html.

g) https://www.youtube.com/watch?v=VK6WXlgosNk dělení komplexních čísel v gon. tvaru

h) https://pl.wikipedia.org/wiki/Liczby_zespolone ładny wykład bez prezentacji filmowej!

https://www.youtube.com/watch?v=icqHFIdPaeY

https://www.youtube.com/watch?v=Gh6OPfuldlM

Na razie tyle

Kolejne przykłady do przestudiowania

5) https://www.matemaks.pl/pierwiastkowanie-liczb-zespolonych.html Wzór de Moivre'a - potęgowanie liczb zespolonych Moivrea

6 https://www.youtube.com/watch?v=jaorPYjbjSw

7) https://cs.wikipedia.org/wiki/Euler%C5%AFv_vzorec Eulerův vzorec

https://www.youtube.com/watch?v=WuaBtDHWrv0 l

8) https://www.youtube.com/watch?v=JS-i682gthA

9) https://pl.wikipedia.org/wiki/Liczby_zespolone

10) http://www.foton.if.uj.edu.pl/documents/12579485/cda7aaf1-8a00-4206-9498-07cd3142e543

11) https://pl.wikipedia.org/wiki/Pr%C4%85d_przemienny

12) https://www.edukator.pl/tik_edukator/Okrag_jednostkowy/index.html

13) https://www.youtube.com/watch?v=WuaBtDHWrv0

Dalej po podstawowym zapoznaniu się z liczbami zespolonymi!

Wzór de Moivre'a – potęgowanie liczb zespolonych

Liczby zespolone z, w∈C, z argumentami odpowiednio: α i β, możemy zapisać w postaci trygonometrycznej

Obliczymy teraz iloczyn tych liczb zapisanych w postaci trygonometrycznej:

Ostatnia równość wynika ze wzorów trygonometrycznych na cosinus sumy kątów oraz na sinus sumy kątów. Powyższy rachunek pokazuje, że przy mnożeniu dwóch liczb zespolonych z, w∈C otrzymujemy liczbę zespoloną, której:

moduł jest iloczynem modułów liczb z oraz w,

argument jest sumą argumentów liczb z oraz w.

Wynika stąd następujący wzór:

Wzór de Moivre'a

Dla dowolnej liczby z∈C zachodzi następujący wzór:

Potęgowanie

Wzór do obliczenia n-tego pierwiastka z liczby zespolonej na podstawie twierdzenia Moivrea

Pierwiastek liczby zespolonej , gdzie a różni się od zera i n jest liczbą całkowitą, potem istnieje właśnie n liczb zespolonych, które są n-tym pierwiastkiem z a, tzn. takich liczb z, że . Są to liczby

gdzie .

Tożsamość Eulera

Euler's formula.svg

Dzielenie liczb zespolonych w postaci algebraicznej

https://www.youtube.com/watch?v=Lh91nkj7IXw

Dzielenie liczb zespolonych w postaci trygonometrycznej i wykładniczej

https://www.youtube.com/watch?v=LL7yq7JZMiI

Wzór ogólny na mnożenie i dzielenie liczb zespolonych w postaci trygonometrycznej

https://eszkola.pl/matematyka/dzialania-na-liczbach-zespolonych-w-postaci-trygonometrycznej-9810.html

Działania na liczbach zespolonych w postaci trygonometrycznej

Liczby zespolone z, w∈C, z argumentami odpowiednio: α i β, możemy zapisać w postaci trygonometrycznej

Dzielenie liczb zespolonych w postaci algebraicznej

https://www.youtube.com/watch?v=Lh91nkj7IXw

Dzielenie liczb zespolonych w postaci trygonometrycznej i wykładniczej

https://www.youtube.com/watch?v=LL7yq7JZMiI

Wzór ogólny na mnożenie i dzielenie liczb zespolonych w postaci trygonometrycznej

https://eszkola.pl/matematyka/dzialania-na-liczbach-zespolonych-w-postaci-trygonometrycznej-9810.html

Działania na liczbach zespolonych w postaci trygonometrycznej

Postać trygonometryczna liczby zespolonej umożliwia bardzo łatwe wykonywanie mnożenia i dzielenia liczb zespolonych. Wykonywanie tych działań na liczbach w postaci algebraicznej wymagało pewnego wysiłku, natomiast dysponując postacią trygonometryczną możemy to zrobić w prostszy sposób.

Niech dane będą dwie liczby w postaci trygonometrycznej:

$z_1=|z_1 |(\cos \alpha +i\sin \alpha )$ oraz $z_2=|z_2 |(\cos \beta +i\sin \beta )$ .

Wówczas:

$z_1 \cdot z_2=|z_1 | \cdot |z_2 |(\cos (\alpha + \beta ) +i\sin ( \alpha + \beta ))$ ,

Jaki będzie wzór ogólny do dzielenia liczb zespolonych w postaci trygonometrycznej?

Będzie podobny i znajdziemy go w

https://eszkola.pl/matematyka/dzialania-na-liczbach-zespolonych-w-postaci-trygonometrycznej-9810.html

https://home.agh.edu.pl/~mariuszp/wfiis_mmf/wyklad_mmf1_1_0809.pdf

Podstawowe wzory liczb zespolonych

https://obliczone.pl/wzory-i-w%C5%82asno%C5%9Bci/636-liczby-zespolone#h14-pulapki-zwiazane-z-jednostka-urojona-nbsp

Zastosowanie w fizyce

https://home.agh.edu.pl/~mariuszp/wfiis_mmf/wyklad_mmf1_1_0809.pdf

Matematické symboly a značky – Lista symboli matematycznych

https://cs.wikipedia.org/wiki/Matematick%C3%A9_symboly_a_zna%C4%8Dky

https://pl.wikipedia.org/wiki/Lista_symboli_matematycznych

Na koniec pozwolę sobie podziękować kierownictwu firmy EMTEST sp. z o.o. z Czeskiego Cieszyna za umożliwienie przeprowadzenia prelekcji, w jej pokoju konferencyjnym, dla członków Stowarzyszenia Elektrotechników Polskich w Republice Czeskiej.

Bogusław Kaleta

Dobór kabli i przewodów w instalacjach elektrycznych

W 2011 roku Parlament Europejski i Rada Unii Europejskiej przyjęły rozporządzenie nr 305/2011 z 9.3.2011 r., ustanawiające zharmonizowane warunki wprowadzania do obrotu wyrobów budowlanych. Jako jedną z grup wyrobów objętych rozporządzeniem wymieniono kable zasilania, sterujące i komunikacyjne. Mimo, że od wejścia w życie tego przepisu upłynęło sporu czasu, pojawiają się nadal wątpliwości, kontrowersje i niedomówienia dotyczące doboru i stosowania kabli oraz przewodów ze względu na ich reakcję na ogień. Nie zawsze pamięta się przy tym, że zasady, jakie stosuje się przy projektowaniu, budowie i przebudowie oraz zmianie użytkowania budynków oraz budowli spełniających funkcje użytkowe są określone w przepisach i normach technicznych.

Terminologia: Zarówno w polskim tłumaczeniu rozporządzenia europejskiego, jak i w rozporządzeniu Ministerstwa Infrastruktury i Budownictwa użyto określenia „kable zasilające, sterujące i komunikacyjne“, z kolei w Warunkach Technicznych używane są określenia „przewody i kable elektryczne“ itp. W celu usystematyzowania terminologii stosowane są określenia zgodne z PN-E-01002:1997:

kable i przewody elektroenergetyczne (kable zasilające, kable i przewody elektryczne),

kable sterownicze (kable sterujące, stosowane w systemach sterowania),

kable i przewody telekomunikacyjne (kable telekomunikacyjne, kable i przewody telekomunikacyjne, w tym kable światłowodowe).

W normach występuje określenie: oprzewodowanie – to zestaw składający się z gołych lub izolowanych przewodów, kabli lub szyn zbiorczych wraz z elementami mocującymi oraz w razie potrzeby, osłonami przewodów, kabli lub szyn.

Występuje również termin „osłony do ochrony kabli zasilających, kabli sterujących i kabli komunikacyjnych“, przy czym brakuje definicji tego określenia. Logicznym wydaje się zastosowanie takiej samej definicji i uznania za osłony systemów: rur, listew, korytek i drabinek instalacyjnych.

Rozporządzenie polskiego Ministerstwa Infrastruktury i Budownictwa nałożyło określone obowiązki na producentów, importerów i dystrybutorów wprowadzające do obrotu wyroby budowlane w całej Unii Europejskiej. Określono w nim m.in.: a) sposób deklarowania właściwości użytkowych wyrobów budowlanych, b) krajowe systemy oceny i weryfikacji stałości właściwości użytkowych wyrobów budowlanych, c) grupy wyrobów objętych obowiązkiem sporządzania krajowej delegacji właściwości użytkowych oraz właściwe dla tych grup krajowe systemy oceny i weryfikacji stałości właściwości użytkowych oznaczone 1+, 1, 2+, 2, 3, 4 (od najbardziej do najmniej wymagającego).

Klasy reakcji na ogień kabli i przewodów: A_CA, B1_CA, B2_CA, C_CA, D_CA, E_CA, F_CA odpowiadają przyjętym zasadom w rozporządzeniu Komisji Europejskiej 2016/364. Część z nich (klasy B1_CA, B2_CA, C_CA i D_CA) dodatkowo podzielono zgodnie z normą PN-EN 13501-6:2019 na podklasy (klasy dodatkowe, grupy) ze względu na:

wydzielanie dymu (s1, s1_A, s1_B, s2, s3),

płonące krople i/ lub cząsteczki (d0, d1, d2),

kwasowość (a1, a2 a3).

Im mniejsza liczba, tym ostrzejszy wymóg. Przykładowe oznaczenia klasy kabla lub przewodu: B2_CA-s2,d1,a3.

Mimo, iż w rozporządzeniu Ministerstwa Infrastruktury i Budownictwa o właściwościach wyrobów budowlanych określono klasy reakcji na ogień dla osłon do ochrony kabli i przewodów takich, jak systemy rur, listew, korytek i drabinek instalacyjnych stosowanych w obiektach budowlanych, to brak jest norm określających wymagania, metody badań i oceny, pozwalających na klasyfikację ich reakcji na ogień.

Źródło: INPE, nr 262-263, str. 53-57

Spis treści

Okładka (Vysoká škola báňská – Technická univerzita w Ostrawie) 1

Protokół ze zebrania członkowskiego SEP – 15.4.2021 r. 2

Spotkanie członkowskie SEP – 21.10.2021 r. 2

Spotkanie elektryków z prelekcją – 25.11.2021 r. 3

VŠB-Technická univerzita: absolwenci o zatrudnienie w branży 4-5

obawiać się nie muszą

Przeczytaliśmy: Oszczędzamy, aby płacić (trochę) mniej 5-6

Bogusław Kaleta. Matematyka, niezbędne narzędzie elektrotechniki 7-29

Dobór kabli i przewodów w instalacjach elektrycznych 30

Apel do członków SEP i społeczności w Polsce w sprawie włączenia 31

się w walkę z koronawirusem

Okładka (Przyrządy kleszczowe do pomiaru oporu uziemienia 32

C.A 6416 i C.A 6417, producent CHAUVIN ARNOUX GROUP)

Apel do członków SEP i społeczności elektryków w Polsce

w sprawie włączenia się w walkę z koronawirusem

Zamieszczamy apel Stowarzyszenia Elektryków Polskich, podpisany przez prezesa Zarządu Głównego SEP w Warszawie, Piotra Szymczaka i zamieszczony w polskich mediach.

Koleżanki i Koledzy! Szanowni Państwo! Od wielu miesięcy żyjemy w sytuacji przewlekłego stresu, który spotęgowany jest dalszym, nieprzewidywalnym przebiegiem i skutkami pandemii Covid-19. Doświadczamy obawy o własne życie i zdrowie, a co najważniejsze – naszych bliskich. Emocje te są spotęgowane przez informacje pojawiające się w mediach. Są one często niepełne. Czasem sprzeczne. Nie wiemy, kiedy pandemia się skończy. Ale dziś mamy już realną broń – są nią szczepienia. Wszyscy tęsknimy za normalnością, za powrotem do tradycyjnej, nielimitowanej pandemicznymi ograniczeniami pracy, za podróżami i spotkaniami. W tym ma pomóc szczepionka. Staniemy się bezpieczni dla siebie, naszych rodzin i całego otoczenia. Apelujemy więc o zaszczepienie się. Razem postarajmy się przekonać do wzięcia udziału w akcji szczepień jak największą grupę naszych Koleżanek i Kolegów, współpracowników, przyjaciół i znajomych.

Jesteśmy przekonani, że upowszechniając na naszych stronach internetowych lub profilach społecznościowych niniejszy apel i prośby o zachowanie bezpiecznego dystansu w miejscach publicznych, a przede wszystkim – szczepiąc się przeciw Covid-19, będziemy mogli dotrzeć do szerokiego grona odbiorców. Branżowa jedność umocni nasze wspólne wysiłki w walce z Covid-19.

W Stowarzyszeniu Elektryków Polskich w marcu 2021 r. powołano Zespół Koordynacyjny SEP ds. Walki z Koronawirusem pod kierownictwem prof. Aleksandra Sieronia. Głównym celem działania Zespołu jest połączenie i koordynacja wysiłku medyków i elektryków, aktywnie działających w Radzie Naukowo-Technicznej SEP. Ten interdyscyplinarny Zespół skoncentrowany jest na opracowywaniu nowych rozwiązań z obszarów elektrotechniki i medycyny do walki z pandemią i jej skutkami, a także do poprawy funkcjonowania społeczeństwa w rzeczywistości post-covidowej.

Zdajemy sobie sprawę, że udział w tegorocznym Międzynarodowym Dniu Elektryka realizowanym w trybie zdalnym wymagał często kompromisowego podejścia i cierpliwości technicznej, ale jesteśmy pewni, że każda rozmowa, spotkanie, wymiana myśli jest ważna, zawsze potrzebna i przynosi dobre owoce. Miejmy nadzieję, że konieczność spotkania jedynie w trybie online będzie w przyszłości kwestią wyboru, a nie koniecznością.

Życzymy Państwu, wszystkim Koleżankom i Kolegom przede wszystkim dużo zdrowia i do zobaczenia za rok – już w tradycyjnej formule!

Przyrządy kleszczowe do pomiaru oporu uziemienia produkuje francuska firma CHAUVIN ARNOUX GROUP. Na zdjęciu najnowsze wersje C.A 6416 i C.A 6417

„Biuletyn Internetowy SEP“ – BIULETYN SEP numer 49, wydawca: Sdružení polských elektrotechniků v České republice / Stowarzyszenie Elektrotechników Polskich w Republice Czeskiej (SEP), zamknięcie numeru: 17.12.2021 r., adres wydawnictwa: 737 01 Český Těšín (Czeski Cieszyn), ul. Střelniční (Strzelnicza) 28/209, redaktor: inż. Tadeusz Toman, 737 01 Třinec-Konská (Trzyniec-Końska) 49, wydano w formie zeszytu dla członków SEP (gratis) i elektronicznie na http://www.coexistentia.cz/SEP/index.html